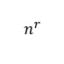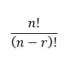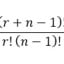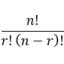Aunque el metajuego de Clash Royale nos indica que sólo es posible usar unas pocas barajas, lo cierto es que la enorme cantidad de cartas nos permitiría hacer uso de una auténtica barbaridad de combinaciones distintas. 297,202,526,775 mazos distintos podrían usarse en el título de estrategia en tiempo real de Supercell.
El usuario de reddit Aggravating Union480 es el autor de este increíble cálculo, realizado teniendo en cuenta la existencia de las 106 cartas que componen el juego, y que nosotros os pasamos a explicar ahora mismo.
Combinaciones y Permutaciones
|
Se repiten |
No se repiten |
|
|
Permutaciones |
 |
 |
|
Combinaciones |
 |
 |
Para empezar, tendríamos que explicar la existencia de una rama de la matemática como es la combinatoria. Este área de dicha ciencia se dedica al cálculo de todo tipo de combinaciones y engloba dos grupos más pequeños de cálculos: las permutaciones y combinaciones.
La primera de ellas es el cálculo de todas las combinaciones cuando el orden importa, como por ejemplo el número de un candado, donde 253 puede abrirlo y 352 no a pesar de tener los mismos números. La segunda, las combinaciones propiamente dichas, serían como combinaciones de colores en un óleo o piezas de fruta en una cesta; el orden nos da igual. A estas dos, se les puede añadir un subtipo, como es el poder o no elegir de nuevo algo que ya hemos elegido.
Arriba tenéis las fórmulas para calcular cada uno de estos cuatro tipos de combinatorias, teniendo siempre en cuenta que "r" es el número de cosas que seleccionas, mientras "n" es el número total de ítems disponibles.
Las peculiaridades de Clash Royale
En base a esto, Clash Royale y sus cartas responderían a una combinación sin repeticiones, es decir, nos da igual el orden, pero no podremos tener dos PEKKAS en el mismo mazo. Parece obvio entonces, que hemos de usar la fórmula de la esquina inferior derecha. Sin embargo, no es tan simple.
Esto sí que era así hasta hace un tiempo, pero la llegada de los campeones lo cambió todo. La Reina Arquera, El Caballero Dorado y El Rey Esqueleto no pueden compartir barajas. Sólo es posible contar con una de estas cartas en nuestro mazo, lo que hace el cálculo algo más complejo.
Si usamos la fórmula anteriormente citada para el resto de cartas, 103, llegamos a 237,762,021,420 barajas distintas sin contar los campeones. A estos habría que añadirles su contribución asumiendo que eliges al menos uno de ellos, pasando a elegir 1 de los otras 103 cartas que no son campeones. Es posible calcularlo para uno, que son 19,813,501,785 barajas adicionales, y multiplicar por los tres campeones que hay: 59,440,505,355. Sumamos este último dato y llegamos a las 297,202,526,775 mazos distintos de Clash Royale.
El usuario de Reddit aún va más lejos. Según él, al suponer que cada jugador que descarga el juego usa un mazo único (lo que en realidad está lejos de ser el caso, ya que miles de jugadores juegan de forma idéntica y muchos aún no tienen todas las cartas desbloqueadas), nos arroja una dura verdad. Suponiendo que juegan el 100% de los usuarios que se han descargado, y contando las 501 millones de descargas en Play Store, estima que sólo se han jugado el 1.4% de los mazos posibles de forma consistente.
El cálculo es en realidad algo absurdo, ya que algunos mazos creables son en realidad injugables por el metajuego (mazos demasiado caros, solo con hechizos, o con tropas del mismo coste). Nos recuerda, sin embargo, que siempre es posible innovar y que Supercell tiene espacio para mejorar el metajuego.
Los monstruos coleccionables de Nintendo y Game Freak tienen una apariencia adorable, pero detrás de ellos hay un infierno de matemáticas. Te lo detallamos a continuación.
